The first part of this presentation describes the data structure used to represent typed nested conceptual graphs [Chein and Mugnier, 1997] in memory. While you don't have to perfectly know this data structure in order to use the library (it is possible to use the class cogitant::Graph without having to know what data structures are actually used), it is better to have a sight on these structures in order to better understand the functioning of the library. The second part precisely describes methods available in the class of conceptual graphs representation, while the third describes mechanisms available to browse the various objects (concepts, relations, etc.) forming a graph. Finally, the last section describes how coreference links are handled.
A conceptual graph (cogitant::Graph) is represented as a set of nodes (cogitant::GraphObject) and a set of edges (cogitant::Edge). More precisely, a conceptual graph contains objects that can be instances of different classes (subclasses of cogitant::GraphObject). Each object of a graph is identified in a unique way by the cogitant::iSet which marks that object in the set of objects. These objects are accessible by calling the method cogitant::Graph::nodes() which returns the Set<GraphObject*> containing the objects, or simply by using the cogitant::Graph::nodes(iSet) method that returns the object corresponding to the passed identifier. Several classes are used to represent a conceptual graph:
To each object (identifier i) is associated a set of cogitant::Edge (obtained calling to the cogitant::Graph::edges(iSet) method and passing i as a parameter) which represents the links of this object with other objects of cogitant::Graph. These links are stored in the form of a data structure that contains the link label (cogitant::Edge::m_label, of type cogitant::Edge::Label) and the extremity (cogitant::Edge::m_end). The link origin is not explicitly represented as such a link is always associated with an object which is the link origin. Labels of these links enable to represent parent/child relations (cogitant::Edge::PARENT and cogitant::Edge::CHILD) as well as edges labeled in the sense of conceptual graphs (i.e. labeled by positive integers). For example, the conceptual graph in Figure 1 is represented in memory by a data structure such as that shown in Figure 2.

In the machine representation of a conceptual graph, there is always a root (whose identifier is returned by cogitant::Graph::root()). Although not shown in Figure 2, the root object has an Edge representing a PARENT link to an identifier object ISET_NULL. This root, of type cogitant::InternalGraph, has as a daughter the concepts and relations of the graph of level 0. The phrase "has as daughter" means here the existence of links labeled CHILD associated with the InternalGraph and having the concepts and relations at the extremity, as well as links labeled PARENT associated with the concepts and relations and having the InternalGraph at the extremity. The edges (in the sense of "conceptual graph model") between concepts and relations are represented by Edge associated with cogitant::Concept and cogitant::Relation, having as a label the edge label and as an extremity the linked vertex. Note that there is a PARENT link between A and B if and only if there is a CHILD link between
B and A and there is a link n (n natural integer) between A and B if and only if there is a link n between B and A .
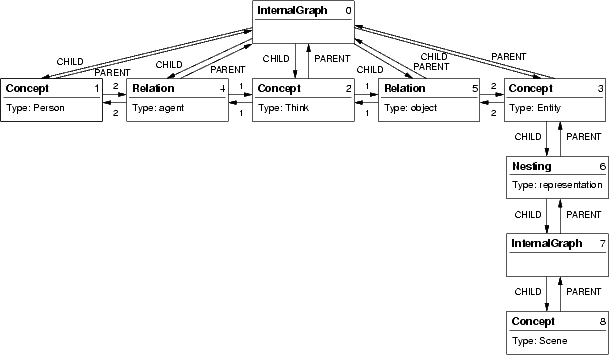
If a concept vertex has nestings (as the vertex 3 in Figure 2), their daughters will be the corresponding cogitant::Nesting. These objects have each of them one and only one daughter which is a cogitant::InternalGraph. These internal graphs obviously have as daughters the concepts and relations of the nested graph. When a graph is built "empty" (by cogitant::Graph, which is called by cogitant::Environment::newGraph), it actually contains a cogitant::InternalGraph, in this way, it is possible to immediately add vertices to the object.
To add a new generic concept vertex to a graph, you have to call the cogitant::Graph::newGenericConcept() method. This method is actually overloaded and can be called by passing as a parameter the identifier (in the support) of concept type, or the type label string. A second optional parameter can be passed to this method: the identifier in the graph of the cogitant::InternalGraph which will get the built vertex as a daughter. If no identifier is passed, the built vertex is daughter of the root, which makes it possible to manipulate basic graphs without considering parent/child links. These methods, like other methods (below-cited) for adding objects in the graph return the identifier of the created object.
The addition of an individual concept vertex is done by calling the cogitant::Graph::newIndividualConcept method that takes as parameters the type identifier, the marker identifier and (possibly) the InternalGraph parent identifier. This method can also be called by passing the label strings of the concept type and the marker.
To add a relation vertex, you have to call the cogitant::Graph::newRelation method which takes as a parameter the relation type identifier (or the type label string), an optional vector<iSet> representing the relation neighborhood to be created and (optionally) the InternalGraph parent identifier. If no vector<iSet> is passed, the edges linked to the relation are "pending". However, if a vector v is passed, an edge labeled 1 is created from the relation to the concept vertex of identifier v[0], an edge labeled 2 to the vertex v[1], and so on. Obviously, the passed vector must have a size of the relation arity, and the vector elements must be concept vertex identifiers having as a parent the same InternalGraph than the one in which the relation is created. To create a binary relation, the cogitant::Graph::newBinaryRelation() method can be used and does not require the use of a vector: identifiers of concept vertices being neighbor to the relation to be create are directly passed to the method.
The addition of a nesting to a concept vertex, is done in a comparable manner, by the cogitant::Graph::newNesting() method which takes as a parameter the nesting type identifier (or the string) and the parent concept identifier. Caution: the call to this method does not create a daughter cogitant::InternalGraph, which must be explicitly created by a call to cogitant::Graph::newInternalGraph() which takes as a parameter the parent nesting identifier.
Example. The graph in Figure 1 is created in memory after having loaded the corresponding support from a BCGCT file.
The built graph being displayed on the screen, the execution of this program returns the display below. The analysis of the display shows the graph structure, and more particularly parent (referred to as P) / child (referre to as C) relations. The structure given in Figure 2 can be found in exactly this display: the object of identifier 0 has as daughters the objects 1, 2, 3, 4, 5, there is an Edge from 2, labeled 1 and pointing to 4, and so on.
Removing graph nodes is done by calling the cogitant::Graph::deleteObject(iSet) method, which takes as a parameter the identifier of a node to be destroyed. If the node has children, they are also destroyed (recursively). If the destroyed object is a concept vertex, any edge linked to this vertex are made pending.
The cogitant::Graph::link() method enables the linking of a relation vertex to a concept vertex. More precisely, this method must get as parameters the identifier of a relation vertex, an edge label (i.e. an unsigned int comprised between 1 and the relation arity) and the identifier of a concept vertex. If an edge corresponding to the passed label already exists among the relation Edges, it is "unbound" from its previous extremity to be linked to the passed concept vertex.
Joining two concept vertices of the same label and having no nestings can be done by the cogitant::Graph::joint(iSet,iSet) method which takes as parameters the vertex identifiers. After the execution of this method, only the identifier of the first vertex is still valid, as the object of the second identifier has been deleted. cogitant::Graph::merge() provides a better control on the fusion of two concept nodes.
After changing the type of a relation vertex (with a call to the cogitant::Relation::setType() method), the arity relation may change. In this case, you have to call the cogitant::Graph::recreateNeighbourhood() method which takes as a parameter a relation vertex identifier. This method may create pending edges (when the new type arity is greater than the previous type) or removes supernumerary edges (otherwise).
Objects forming the cogitant::Graph structure can be accessed through the cogitant::Graph::nodes() method which returns a (pointer to a) set of (pointers to) cogitant::GraphObject. This class is actually an abstract class, the mother of all classes that can represent graph nodes. More particularly, cogitant::InternalGraph and cogitant::LabeledGraphObject classes derive from this class. The cogitant::LabeledGraphObject class is an abstract class which enables to factorize properties common to objects labeled: cogitant::Concept, cogitant::Relation, cogitant::Nesting.
Accessing graph components being done through GraphObject* objects, you cannot therefore call on these objects methods of its subclasses. You can know from which class an object is instance of by calling the cogitant::GraphObject::objectType() method which returns a cogitant::GraphObject::Type, which is an enumerated type taking values OT_CONCEPT, OT_RELATION, OT_NESTING and OT_INTERNALGRAPH. By using this information, you can thus explicitly and safely convert a GraphObject* into a Concept*, etc. Nevertheless, you should rather use methods cogitant::GraphObject::asConcept(), cogitant::GraphObject::asRelation(), cogitant::GraphObject::asNesting() and cogitant::GraphObject::asInternalGraph() which return a pointer to, respectively, a Concept, a Relation, a Nesting, an InternalGraph. These methods first ensure that the conversion is permitted (otherwise, an exception is raised) before returning a pointer of the desired type.
The different classes corresponding to graph objects have methods that can modify objects, for example:
In many cases, you need to traverse objects of a graph, and very often, you need to only traverse certain object types (only concept vertices, only level 0 graph relations, etc.). Traversing all concept vertices of a graph can be done for example by the following program, which uses only methodes of the cogitant::Set class.
However, it is easier to use methods provided in the cogitant::Graph class and which enable a selective traversal on objects. So, methods cogitant::Graph::conceptBegin() and cogitant::Graph::conceptEnd(), cogitant::Graph::relationBegin() and cogitant::Graph::relationEnd()... return iterators of a particular type (cogitant::Graph::concept_iterator, cogitant::Graph::relation_iterator, etc.) which enable a simplified traversal of the chosen object type. In this way, the example program above can be rewrited in the following manner:
Methods xxxBegin and xxxEnd accept an optional parameter which is the identifier of the object whose daughters have to be traversed. If this parameter is omitted (or if ISET_NULL is passed), all objects of the chosen type are traversed: in the case of a nested graph, all concept vertices (for example) are traversed. The program example below shows the use of this feature: only concept vertices of the level 0 graph (those which are daughters of the root) are traversed, which corresponds, in the case of the graph in Figure 1, to the concept vertices Person, Think, Entity.
Coreference links are not explicitly represented between concept vertices, but through coreference classes. More precisely, a coreference class contains a set of concept vertices in coreference: if there is a coreference link between A and B, and that there is a same link between B and C, then these three vertices are coreferent, they belong to the same coreference class. In the data structure representing a conceptual graph, it is represented as an instance of cogitant::CoreferenceClass that appears in the set of graph objects (cogitant::Graph::nodes()). This object has ISET_NULL as a parent and has a link (cogitant::Edge) to all concept vertices belonging to the class. Each of these links is labeled by cogitant::Edge::COREFERENCE and also exists in the direction of concept vertex to coreference class.
Only "non-trivial" coreference classes are represented: at the creation of a concept vertex, whatever its label, the vertex belongs to the coreference class formed of this single vertex. Such classes are not represented.
Using methods available from the cogitant::Graph class makes it possible to use coreference links regardless of the representation in memory, even if it is recommended to know the data structures in order to use certain operations.
Each coreference class is marked with a unique name (a string used for saving in BCGCT or CoGXML) and when creating a new coreference class, by calling the cogitant::Graph::newCoreferenceClass() method, you can pass a string to set the name of the created class. If no string is passed, a (unique) name will be automatically assigned. This method returns the identifier of the created class.
This identifier can then be used to add objects to the coreference class: the cogitant::Graph::addCoreference(iSet,iSet) method accepts two parameters: a generic vertex identifier and a coreference class identifier. This method adds the concept vertex to the coreference class provided this vertex does not already belong to a coreference class (a vertex can only be in a single coreference class, but you can merge two coreference classes using the cogitant::Graph::fusionCoreferenceClasses() method). An additional condition must be met in order to call this method: all concept vertices of a coreference class must be generic and of the same type. Otherwise, a cogitant::ExceptionStructure is raised.
To remove a concept vertex of a coreference class, just call the cogitant::Graph::removeCoreference(iSet,iSet) method, which takes as a parameter the concept vertex identifier and the identifier of its coreference class. Finally, to access the coreference class that owns a concept vertex, you can call the cogitant::Graph::coreferenceClass(iSet) method, which takes as a parameter a concept vertex identifier and returns the coreference class identifier at which it belongs or ISET_NULL if the vertex does not belong to any coreference class.
Coreference classes are obviously taken into account when calculating projections in accordance with the model: two vertices of a same coreference class should have as an image either a single vertex, or two vertices having the same individual marker, or two vertices of the same coreference class.
Example. Loading a support, and creating a conceptual graph representing "a person thinking about a scene describing the same person". To represent the fact that it is the same person, a coreference link is created between the two concept vertices "Person". More precisely, a coreference class is created and the two concept vertices are attached to this class.
The program execution leads to the following display, which allows you to note that the coreference link between a concept vertex and its coreference class is represented by "=" when displaying variables of the cogitant::Edge type.
Finally, you can use the coreference without handling coreference classes: the cogitant::Graph::addCoreferenceLink(iSet,iSet) method takes as parameters two concept vertex identifiers and creates the data structures corresponding to the addition of a coreference link between these two vertices. This operation can create a coreference class (if none of the vertices already belongs to such a class), add a vertex to a coreference class (if one of the two vertices belongs to a coreference class but not the other) or merge two coreference classes (if both vertices already belong to distinct coreference classes).