La première partie de cette présentation décrit la structure de données utilisée pour représenter des graphes conceptuels emboîtés typés [Chein et Mugnier, 1997] en mémoire. S'il n'est pas obligatoire de connaître parfaitement cette structure de données pour utiliser la bibliothèque (il est possible d'utiliser les méthodes de la classe cogitant::Graph sans chercher à savoir quelles structures de données sont effectivement utilisées), il est préférable d'avoir une vue de ces structures pour mieux comprendre le fonctionnement de la bibliothèque. La deuxième partie décrit justement les méthodes disponibles sur la classe de représentation des graphes conceptuels, alors que la troisième décrit les mécanismes offerts pour parcourir les différents objets (concepts, relations, etc) qui composent un graphe. Enfin la dernière partie décrit la façon dont les liens de coréférence sont manipulés.
Un graphe conceptuel (cogitant::Graph) est représenté sous la forme d'un ensemble de noeuds (cogitant::GraphObject) et d'un ensemble d'arêtes (cogitant::Edge). Plus précisément, un graphe conceptuel contient des objets qui peuvent être instances de différentes classes (sous-classes de cogitant::GraphObject). Chaque objet d'un graphe est identifié de façon unique par le cogitant::iSet qui repère cet objet dans l'ensemble des objets. Ces objets sont accessibles en appelant la méthode cogitant::Graph::nodes() qui retourne le Set<GraphObject*> contenant les objets, ou plus simplement grâce à la méthode cogitant::Graph::nodes(iSet) qui retourne l'objet correspondant à l'identificateur passé. Plusieurs classes sont utilisées pour représenter un graphe conceptuel :
À chaque objet (d'identificateur i) est associé un ensemble de cogitant::Edge (obtenu par appel à la méthode cogitant::Graph::edges(iSet) en passant i comme paramètre) qui représente les liens de cet objet avec les autres objets du cogitant::Graph. Ces liens sont mémorisés sous la forme d'une structure de donnée qui contient l'étiquette du lien (cogitant::Edge::m_label, de type cogitant::Edge::Label) et l'extrémité (cogitant::Edge::m_end). L'origine du lien n'est pas explicitement représentée car un tel lien est toujours associé à un objet qui est l'origine du lien. Les étiquettes de ces liens permettent de représenter des relations parent/enfant (cogitant::Edge::PARENT et cogitant::Edge::CHILD) ainsi que des arêtes étiquetées au sens des graphes conceptuels (c'est-à-dire étiquetées par des entiers positifs). Ainsi, le graphe conceptuel de la figure 1 est représenté en mémoire par une structure de données telle que celle présentée en figure 2.

Dans la représentation machine d'un graphe conceptuel, il y a toujours une racine (dont l'identificateur est retourné par cogitant::Graph::root()). Même si ce n'est pas représenté sur la figure 2, l'objet racine a une Edge qui représente un lien PARENT vers un objet d'identificateur ISET_NULL. Cette racine, de type cogitant::InternalGraph, a pour fils les concepts et relations du graphe de niveau 0. L'expression "a pour fils" désigne ici l'existence de liens étiquetés CHILD associés à l'InternalGraph et ayant pour extrémité les concepts et relations, ainsi que des liens étiquetés PARENT associés aux concepts et relations et ayant pour extrémité l'InternalGraph. Les arêtes (au sens "modèle des graphes conceptuels") entre concepts et relations sont représentées par des Edge associées aux cogitant::Concept et cogitant::Relation, ayant pour étiquette l'étiquette de l'arête et pour extrémité le sommet lié. À noter que il existe un lien PARENT entre A et B si et seulement si il existe un lien CHILD entre B et A et il existe un lien n (n entier naturel) entre A et B si et seulement si il existe un lien n entre B et A .
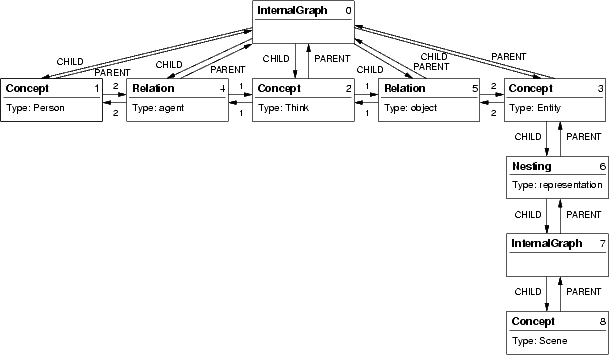
Si un sommet concept possède des emboîtements (comme le sommet 3 dans la figure 2), il a pour fils les cogitant::Nesting correspondants. Ces objets ont chacun un et un seul fils qui est un cogitant::InternalGraph. Ces graphes internes ont évidemment pour fils les concepts et relations du graphe emboîté. Quand un graphe est créé "à vide" (par le constructeur de cogitant::Graph, qui est appelé par cogitant::Environment::newGraph), il contient en fait un cogitant::InternalGraph, de cette façon, il est possible d'ajouter immédiatement des sommets à l'objet.
Pour ajouter un nouveau sommet concept générique à un graphe, il faut appeler la méthode cogitant::Graph::newGenericConcept(). Cette méthode est en fait surchargée et peut être appelée en passant comme paramètre l'identificateur (dans le support) du type de concept, ou la chaîne de caractères de l'intitulé du type. Un deuxième paramètre optionnel peut être passé à cette méthode : l'identificateur dans le graphe du cogitant::InternalGraph qui recevra comme fils le sommet créé. Si aucun identificateur n'est passé, le sommet créé est fils de la racine, ce qui permet de manipuler des graphes simples sans considérer les liens parent/enfant. Ces méthodes, comme les autres méthodes d'ajout d'objets dans le graphe décrites ci-dessous retournent l'identificateur de l'objet créé.
L'ajout d'un sommet concept individuel se fait en appelant la méthode cogitant::Graph::newIndividualConcept qui prend comme paramètres l'identificateur du type, l'identificateur du marqueur et (éventuellement) l'identificateur de l'InternalGraph parent. Cette méthode peut aussi être appelée en passant les chaînes de caractères des intitulés du type de concept et du marqueur.
Pour ajouter un sommet relation, il faut appeler la méthode cogitant::Graph::newRelation qui prend comme paramètre l'identificateur du type de relation (ou la chaîne de l'intitulé du type), un éventuel vector<iSet> représentant le voisinage de la relation à créer et (de façon optionnelle) l'identificateur de l'InternalGraph parent. Si aucun vector<iSet> n'est passé, les arêtes liées à la relation sont "pendantes". Par contre si un vecteur v est passé, une arête d'étiquette 1 est créée de la relation vers le sommet concept d'identificateur v[0], une arête d'étiquette 2 vers le sommet v[1], etc. Évidemment, le vecteur passé doit avoir pour taille l'arité du type de relation, et les éléments du vecteur doivent être des identificateurs de sommets concepts qui ont pour parent le même InternalGraph que celui dans lequel la relation est créée. Pour créer une relation binaire, la méthode cogitant::Graph::newBinaryRelation() peut être utilisée et n'impose pas l'usage d'un vector : les identifiants des sommets concepts voisins de la relation à créer sont directement passés à la méthode.
L'ajout d'un emboîtement à un sommet concept, se fait de façon comparable, par la méthode cogitant::Graph::newNesting() qui prend comme paramètre l'identificateur du type d'emboîtement (ou la chaîne) et l'identificateur du concept parent. Attention, l'appel à cette méthode ne crée pas de cogitant::InternalGraph fils, qui doit explicitement être créé par un appel à cogitant::Graph::newInternalGraph() qui prend comme paramètre l'identifiant de l'emboîtement parent.
Exemple. Le graphe de la figure 1 est créé en mémoire après avoir chargé le support correspondant à partir d'un fichier BCGCT.
Le graphe créé étant affiché à l'écran, l'exécution de ce programme provoque l'affichage donné ci-dessous. L'analyse de cet affichage montre la structure du graphe, et plus particulièrement les relations parent (notées P) / enfant (notées C). La structure donnée dans la figure 2 peut être retrouvée exactement dans cet affichage : l'objet d'identificateur 0 a pour fils les objets 1, 2, 3, 4, 5, il y a une Edge partant de 2, étiquetée 1 et allant vers 4, etc.
La suppression de noeuds d'un graphe se fait en appelant la méthode cogitant::Graph::deleteObject(iSet) qui prend comme paramètre l'identificateur du noeud à détruire. Si ce noeud a des fils, ces fils sont eux aussi détruits (récursivement). Si l'objet détruit est un sommet concept, d'éventuelles arêtes qui étaient liées à ce sommet sont rendues pendantes.
La méthode cogitant::Graph::link() permet de lier un sommet relation à un sommet concept. Plus précisément, cette méthode doit recevoir comme paramètres l'identificateur d'un sommet relation, une étiquette d'arête (c'est-à-dire un unsigned int compris entre 1 et l'arité de la relation) et l'identificateur d'un sommet concept. Si une arête correspondant à l'étiquette passée existe déjà parmi les Edge de la relation, elle est "déliée" de son extrémité précédente pour être liée au sommet concept passé.
Le joint de deux sommets concepts de même étiquette et n'ayant pas d'emboitements peut être effectué par la méthode cogitant::Graph::joint(iSet,iSet) qui prend comme paramètres les deux identificateurs des sommets. Après l'exécution de cette méthode, seul l'identificateur du premier sommet est encore valide, car l'objet correspondant au second identificateur a été supprimé. cogitant::Graph::merge() permet de mieux contrôler la fusion de deux sommets concepts.
Après avoir changé le type d'un sommet de relation (par un appel à la méthode cogitant::Relation::setType()), il est possible que l'arité de la relation change. Dans ce cas, il faut appeler la méthode cogitant::Graph::recreateNeighbourhood() qui prend comme paramètre un identificateur de sommet relation. Cette méthode crée d'éventuelles arêtes pendantes (dans le cas où l'arité du nouveau type est supérieure à celle du type précédent) ou supprime des arêtes surnuméraires (dans le cas contraire).
Les objets composant la structure cogitant::Graph sont accessibles à travers la méthode cogitant::Graph::nodes() qui retourne un (pointeur sur un) ensemble de (pointeurs sur des) cogitant::GraphObject. Cette classe est en fait une classe abstraite, mère de toutes les classes pouvant représenter des noeuds d'un graphe. Plus particulièrement, les classes cogitant::InternalGraph et cogitant::LabeledGraphObject dérivent de cette classe. La classe cogitant::LabeledGraphObject est une classe abstraite qui permet la factorisation des propriétés communes aux objets étiquetés : cogitant::Concept, cogitant::Relation, cogitant::Nesting.
L'accès aux éléments d'un graphe se faisant à travers des GraphObject*, il est donc impossible d'appeler sur ces objets les méthodes des sous-classes. Il est possible de savoir de quelle classe un objet est instance en appelant la méthode cogitant::GraphObject::objectType() qui retourne un cogitant::GraphObject::Type, qui est un type énuméré pouvant prendre les valeurs OT_CONCEPT, OT_RELATION, OT_NESTING et OT_INTERNALGRAPH. En utilisant cette information, il est donc possible de convertir explicitement et sans risque d'erreur un GraphObject* en Concept*, etc. Il est toutefois préférable d'utiliser les méthodes cogitant::GraphObject::asConcept(), cogitant::GraphObject::asRelation(), cogitant::GraphObject::asNesting() et cogitant::GraphObject::asInternalGraph() qui retournent un pointeur sur, respectivement, un Concept, une Relation, un Nesting, un InternalGraph. Ces méthodes vérifient tout d'abord que la conversion est autorisée (et si ce n'est pas le cas, une exception est levée) avant de retourner un pointeur du type désiré.
Les différentes classes correspondant à des objets du graphe disposent de méthodes permettant de modifier les objets, par exemple :
Dans de nombreux cas, il est nécessaire de parcourir les objets d'un graphe, et très souvent, il est nécessaire de parcourir seulement un certain type d'objets (uniquement les sommets concepts, uniquement les relations du graphe de niveau 0, etc). Un parcours de tous les sommets concepts du graphe peut être par exemple effectué par le programme suivant, qui utilise uniquement les méthodes de la classe cogitant::Set.
Il est toutefois plus simple d'utiliser les méthodes fournies dans la classe cogitant::Graph et qui permettent un parcours sélectif des objets. Ainsi, les méthodes cogitant::Graph::conceptBegin() et cogitant::Graph::conceptEnd(), cogitant::Graph::relationBegin() et cogitant::Graph::relationEnd()... retournent des itérateurs d'un type particulier (cogitant::Graph::concept_iterator, cogitant::Graph::relation_iterator, etc.) qui permettent un parcours simplifié du type d'objet voulu. De cette façon, le programme d'exemple ci-dessus peut être réecrit de la façon suivante :
Les méthodes xxxBegin et xxxEnd admettent un paramètre optionnel qui est l'identificateur de l'objet dont les fils doivent être parcourus. Si ce paramètre est absent (ou si ISET_NULL est passé), tous les objets du type voulu sont parcourus : dans la cas d'un graphe emboîté, tous les sommets concepts (par exemple) sont parcourus. L'exemple de programme ci-dessous montre l'utilisation de cette fonctionnalité : seuls les sommets concepts du graphe de niveau 0 (ceux qui sont fils de la racine) sont parcourus, ce qui correspond, dans le cas du graphe de la figure 1, aux sommets concepts Person, Think, Entity.
Les liens de coréférence ne sont pas explicitement représentés entre sommets concepts, mais à travers des classes de coréférence. Plus précisément une classe de coréférence regroupe un ensemble de sommets concepts en coréférence : s'il existe un lien de coréférence entre A et B, et qu'il existe un même lien entre B et C, alors ces trois sommets sont coréférents, ils appartiennent à la même classe de coréférence. Dans la structure de données représentant un graphe conceptuel, ceci est représenté comme une instance de cogitant::CoreferenceClass qui apparaît dans l'ensemble des objets du graphe (cogitant::Graph::nodes()). Cet objet a pour parent ISET_NULL et a un lien (cogitant::Edge) vers tous les sommets concepts qui appartiennent à la classe. Chacun de ces liens est étiqueté par cogitant::Edge::COREFERENCE et existe aussi dans le sens sommet concept vers classe de coréférence.
Seules les classes de coréférence "non triviales" sont représentées : à la création d'un sommet concept, quelle que soit son étiquette, celui-ci appartient à la classe de coréférence formée de ce seul sommet. De telles classes ne sont pas représentées.
L'utilisation des méthodes disponibles à partir de la classe cogitant::Graph permet d'utiliser des liens de coréférence sans se soucier de la représentation en mémoire, même s'il est préférable de connaître les structures de données pour pouvoir utiliser certaines opérations.
Chaque classe de coréférence est repérée par un nom unique (une chaîne de caractères utilisée pour la sauvegarde en BCGCT ou CoGXML) et lors de la création d'une nouvelle classe de coréférence, par appel à la méthode cogitant::Graph::newCoreferenceClass(), il est possible de passer une chaîne de caractères pour choisir le nom de classe créée. Si aucune chaîne n'est passée, un nom (unique) sera automatiquement déterminé. Cette méthode retourne l'identificateur de la classe créée.
Cet identificateur peut ensuite être utilisé pour ajouter des objets à la classe de coréférence : la méthode cogitant::Graph::addCoreference(iSet,iSet) admet deux paramètres : l'identificateur d'un sommet concept générique et l'identificateur d'une classe de coréférence. Cette méthode ajoute le sommet concept à la classe de coréférence à condition que ce sommet n'appartienne pas déjà à une classe de coréférence (un sommet ne peut être que dans une classe de coréférence, mais il est possible de fusionner deux classes de coréférence en utilisant la méthode cogitant::Graph::fusionCoreferenceClasses()). Une condition supplémentaire doit être vérifiée pour pouvoir appeler cette méthode : tous les sommets concepts d'une classe de coréférence doivent être génériques et de même type. Si ce n'est pas le cas, une cogitant::ExceptionStructure est levée.
Pour enlever un sommet concept d'une classe de coréférence, il suffit d'appeler la méthode cogitant::Graph::removeCoreference(iSet,iSet) qui prend comme paramètre l'identificateur du sommet concept et l'identificateur de sa classe de coréférence. Enfin, pour accéder à la classe de coréférence à laquelle appartient un sommet concept, il est possible d'appeler la méthode cogitant::Graph::coreferenceClass(iSet) qui prend comme paramètre l'identificateur d'un sommet concept et retourne l'identificateur de la classe de coréférence à laquelle il appartient ou ISET_NULL si ce sommet n'appartient à aucune classe de coréférence.
Les classes de coréférence sont évidemment prises en compte pour le calcul de projections conformément au modèle : deux sommets d'une même classe de coréférence doivent avoir pour image soit un seul sommet, soit deux sommets ayant même marqueur individuel, soit deux sommets de la même classe de coreférence.
Exemple. Chargement d'un support, et création d'un graphe conceptuel représentant "une personne pensant à une scène décrivant cette même personne". Pour représenter le fait qu'il s'agit de la même personne, un lien de coréférence est créé entre les deux sommets concepts "Person". Plus précisément, une classe de coréférence est créée et les deux sommets concepts sont rattachés à cette classe.
L'exécution de ce programme provoque l'affichage suivant, qui permet de remarquer que le lien de coréférence entre un sommet concept et sa classe de coréférence est représenté par "=" lors de l'affichage de variables de type cogitant::Edge.
Il est possible enfin d'utiliser la coréférence sans manipuler de classes de coréférence : la méthode cogitant::Graph::addCoreferenceLink(iSet,iSet) prend comme paramètres deux identificateurs de sommets concepts et crée les structures de données correspondant à l'ajout d'un lien de coréférence entre ces deux sommets. Cette opération peut provoquer la création d'une classe de coréférence (si aucun des sommets n'appartient déjà à une telle classe), l'ajout d'un sommet à une classe de coréférence (si l'un des deux sommets appartient à une classe de coréférence et l'autre pas) ou la fusion de deux classes de coréférence (si les deux sommets appartiennent déjà à des classes de coréférence distinctes).